Предмет: Алгебра,
автор: mishozzy
решите уравнение логарифмической функции. задание из Алгебра и начало мат.анализа Зив 10-11 классы
Приложения:
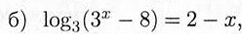
Ответы
Автор ответа:
0
log[3](3^x-8)=2-x
ОДЗ 3^x-8>0
3^x-8=3^(2-x)=3^2/3^x=9/3^x
(3^x)^2-8*3^x-9=0
3^x=y
y^2-8y-9=0
y1= -1--->отбрасываем.
y2=9
3^x=9
x=2
ОДЗ 3^x-8>0
3^x-8=3^(2-x)=3^2/3^x=9/3^x
(3^x)^2-8*3^x-9=0
3^x=y
y^2-8y-9=0
y1= -1--->отбрасываем.
y2=9
3^x=9
x=2
Автор ответа:
0
как в 4строчке получается (3^x)^2?
Автор ответа:
0
Приводим к общему знаменателю (множим на 3^x)
Похожие вопросы
Предмет: Алгебра,
автор: sashavasilyk74
Предмет: Математика,
автор: dyxghcjfif
Предмет: Геометрия,
автор: Аноним
Предмет: География,
автор: лероки
Предмет: Литература,
автор: dino4ka99