Предмет: Геометрия,
автор: thkbfzilä
Извесно , что медиана треугольника есть его высотой. Докажите , что этот треугольник - Равнобедренный
Ответы
Автор ответа:
0
Назовем тругольник АВС, где медиана - АМ. Докажем, что треугольники АВМ и АСМ равны. Так как АМ является высотой, мы можем сказать, что треугольники АВМ и АСМ являются прямоугольными, значит угол АМС=углу АМВ=90 градусов. Так как АМ медиана, значит ВМ=МС. Сторона АМ - общая. Из всего вышесказанного можем сделать вывод, что треугольник АВМ=АСМ по двум сторонам и углу между ними.
Автор ответа:
0
ну и соответственно если треугольники равны, то это значит, что АВ=АС, а значит треугольник АВС равнобедренный. Что и требовалось доказать
Автор ответа:
0
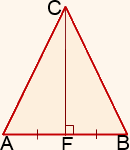
(Фото внизу)
Рассмотрим ∆ AFC и ∆ BFC.
1) ∠AFC=∠BFC=90º (так как CF — высота треугольника ABC по условию).
2) AF=BF (так как CF — медиана треугольника ABC по условию).
3) Сторона CF — общая.
Следовательно, ∆ AFC = ∆ BFC (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон:
AC=BC. Значит, ∆ ABC — равнобедренный с основанием AB (по определению
равнобедренного треугольника). Доказано.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: shapikzanovo
Предмет: Английский язык,
автор: tlepbaeva7018
Предмет: Литература,
автор: abdyldabekovaajzan
Предмет: Математика,
автор: Дианасмайл
Предмет: Математика,
автор: Seminaja