Question

Ребята помогите задачу решить пожалуйста........... Длина касательной, проведенной из некоторой точки к окружности, равна 20 см, а длина наибольшей
секущей, проведенной из этой точки, равна 50 см.Найдите радиус окружности. И чертеж приложите умоляю!!!!

Answer 1

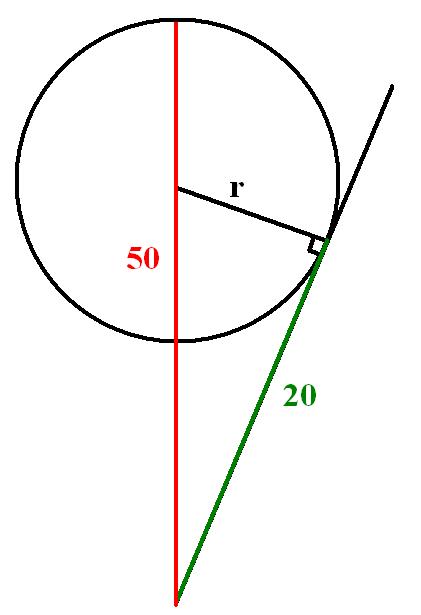
Так как секущая наибольшая, то она проходит через центр окружности.
Так как радиус, проведенный в точку касания перпендикулярен касательной, то применяем теорему Пифагора к образовавшемуся прямоугольному треугольнику:
$(50-r)^2=r^2+20^2 \\\ 2500-100r+r^2=r^2+400 \\\ 100r=2100 \\\ r=21(sm)$
Ответ: 21 см