Предмет: Геометрия,
автор: alphamaster
Как доказать, что треугольники MAD и MCD -прямоугольные?
Приложения:
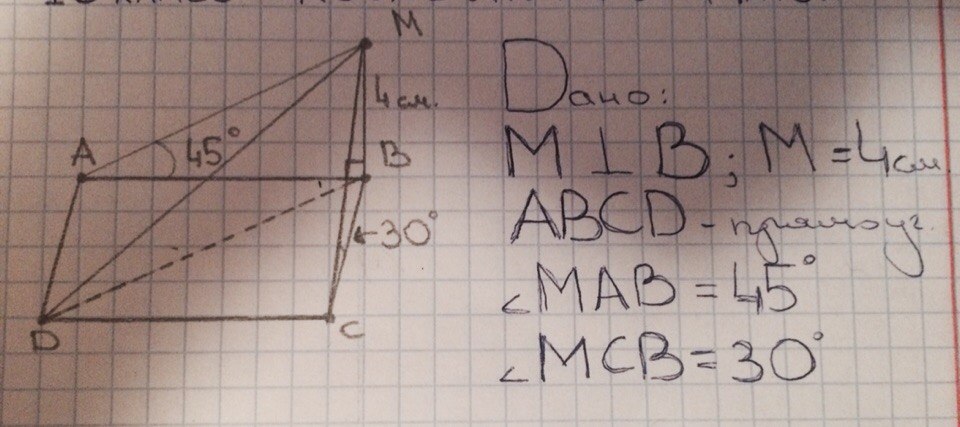
Ответы
Автор ответа:
0
BC⊥BM по условию
BC⊥AB т.к. ABCD - прямоугольник
значит BC ⊥ плоскости ABM
т.к. AD||BC, то AD тоже ⊥ плоскости ABM
Значит AD перпендикулярна отрезку AM, который лежит в плоскости AMB
и проходит через основание перпендикляра. Т.е. угол MAD - 90 градусов.
Аналогично и с углом MCD
Да, и дано там криво записано :)
Что значит M⊥B? Точка перпендиклярна другой точке? :)) только по чертежу и ясно...
И M=4 см. Точка равна 4 см? :)) Думать же надо, что пишешь :)
BC⊥AB т.к. ABCD - прямоугольник
значит BC ⊥ плоскости ABM
т.к. AD||BC, то AD тоже ⊥ плоскости ABM
Значит AD перпендикулярна отрезку AM, который лежит в плоскости AMB
и проходит через основание перпендикляра. Т.е. угол MAD - 90 градусов.
Аналогично и с углом MCD
Да, и дано там криво записано :)
Что значит M⊥B? Точка перпендиклярна другой точке? :)) только по чертежу и ясно...
И M=4 см. Точка равна 4 см? :)) Думать же надо, что пишешь :)
Автор ответа:
0
Да, неловко вышло)
Автор ответа:
0
Спасибо большое ;)
Автор ответа:
0
на здоровье :)
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: ekosh7825
Предмет: Математика,
автор: hodarevasvetlana
Предмет: География,
автор: stella56078
Предмет: История,
автор: Аноним