Предмет: Алгебра,
автор: raverina
!!! Решите уравнение, используя однородность. Подробно, пожалуйста. Заранее спасибо)
Приложения:
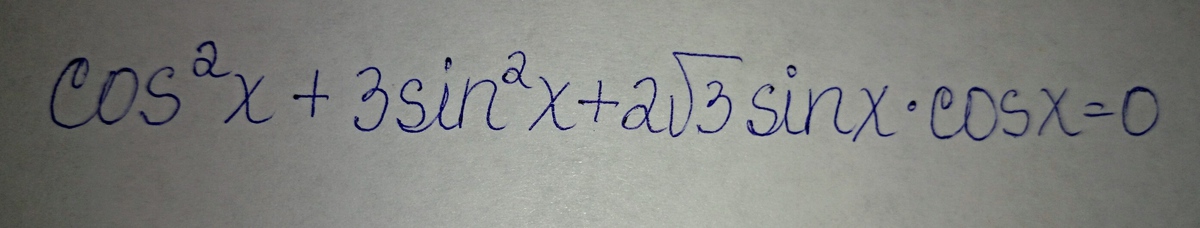
Ответы
Автор ответа:
1
Разделим на cos²x≠0
3tg²x+2√3tgx+1=0
(√3tgx+1)²=0
√3tgx+1=0
tgx=-1/√3
x=-π/6+πn
3tg²x+2√3tgx+1=0
(√3tgx+1)²=0
√3tgx+1=0
tgx=-1/√3
x=-π/6+πn
raverina:
Большое спасибо)
Автор ответа:
2
Разделим на sinx;
n∈Z
Спасибо :-)
Похожие вопросы
Предмет: Английский язык,
автор: sab1no4ka
Предмет: Английский язык,
автор: 116541
Предмет: Английский язык,
автор: Лазалка
Предмет: Литература,
автор: MariaRoy007