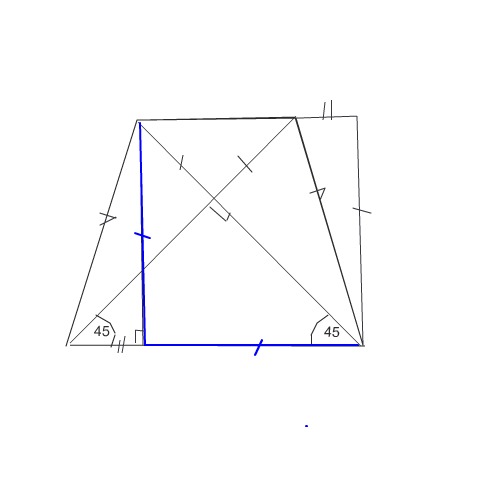
в равнобедренной трапеции диагонали перпендикулярны.Высота 15 см.Найти среднюю линию
Ответы
ABCD – трапеция
О – точка пересечения диагоналей
Проведем высоту MK через точку пересечения диагоналей
Пусть OM=x и OK=y
x+y=15 – по условию
Высота OM делит треугольник BCO на два равнобедренные треугольника
OM=MC=BM => BC=2x
Высота OK делит треугольник AOD на два равнобедренные треугольника
KO=AK=KD =>AB=2y
Средняя линия равна (BC+AD)/2 = (2x+2y)/2=x+y=15
См. рисунок:
Так как диагонали в этой трапеции взаимно перпендикулярны, углы между диагоналями и основаниями трапеции равны 45°.
"Перевернем и перенесем" ( мысленно) прямоугольный треугольник, который высота трапеции отсекает от нее с боковой линией и "приложим" по другую сторону трапеции. Получим квадрат со стороной, равной высоте.
Площадь этого квадрата равна площади трапеции.
Но площадь трапеции находят также произведением ее высоты на среднюю линию.
Следовательно, средняя линия трапеции равна высоте и равна 15 см