Предмет: Геометрия,
автор: undertaker81298
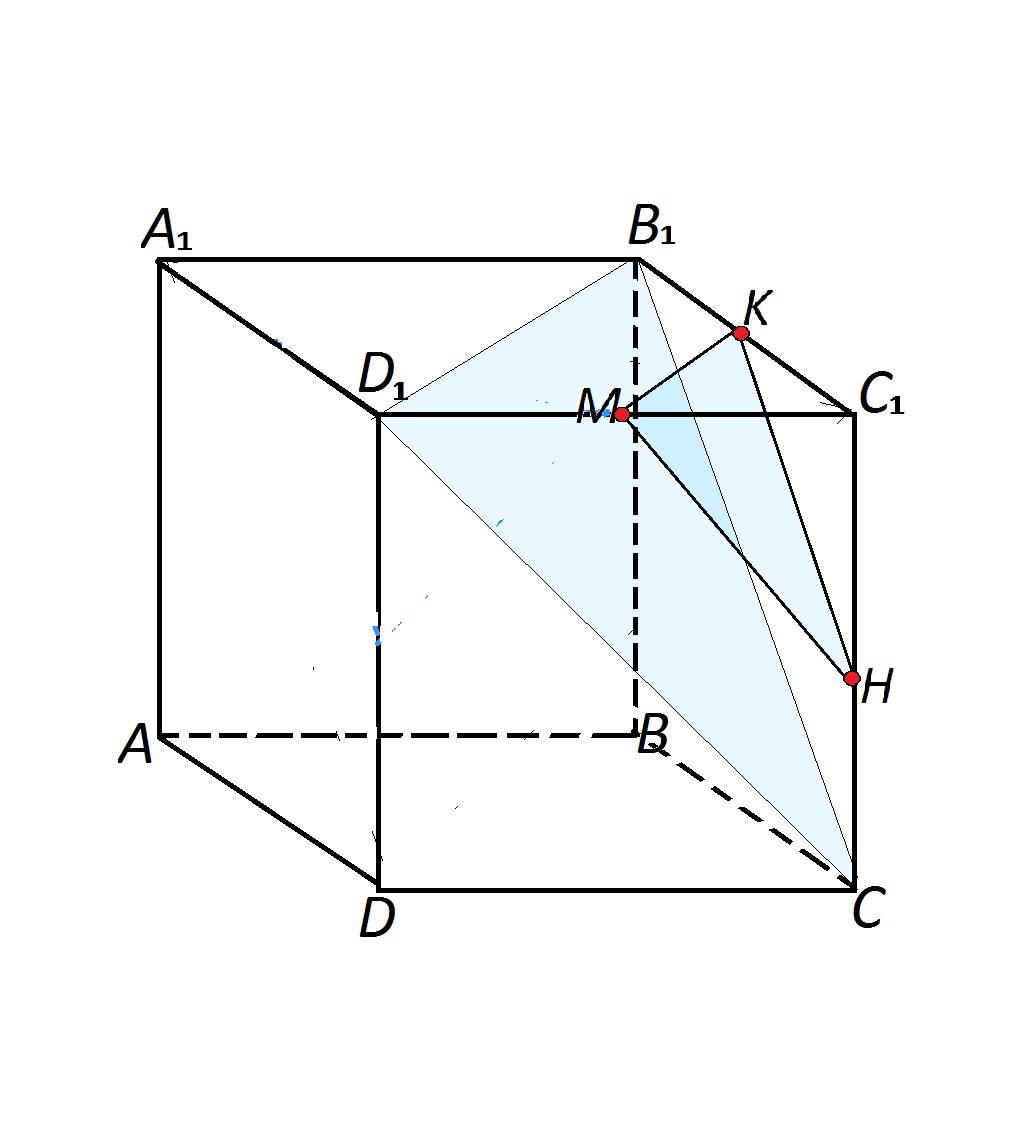
Точка К - середина ребра В1С1 куба АВСDA1B1C1D1. Постройте сечение куба плоскостью, которая проходит через точку К и параллельно плоскости B1CD1. Вычислите площадь поверхности куба, если площадь полученного сечения равна корень3 см^2
Ответы
Автор ответа:
0
Сечение куба B1CD1 - треугольник, т.к. каждая пара его вершин принадлежит одной из граней.
Соответственно и сечение, проходящее через точку К и параллельное плоскости B1CD1 - также треугольник.
Так как его стороны параллельны диагоналям граней куба и проходят через их середины, они равны половине этих диагоналей.
Обозначим сечение МКН. Оно является равносторонним треугольником: МК=КН=МН.
Пусть стороны куба равны а см.
Тогда диагонали граней по формуле диагонали квадрата равны а√2, а стороны сечения МК=(а√2):2
ПлощадЬ правильного треугольника МКН
S=(МК²√3):4
S=(МК²√3):4=√3
S=((а√2):2)²*√3):4=√3
S=(2а²:4)*√3):4=√3
(а²:2)):4=1
а²:8=1
а²=8 - такова площадь одной грани куба.
S полной поверхности куба равна 6а²=8*6=48 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: dariaandreevna287
Предмет: Литература,
автор: ritamefedova3
Предмет: Химия,
автор: Ангелина2330