Question

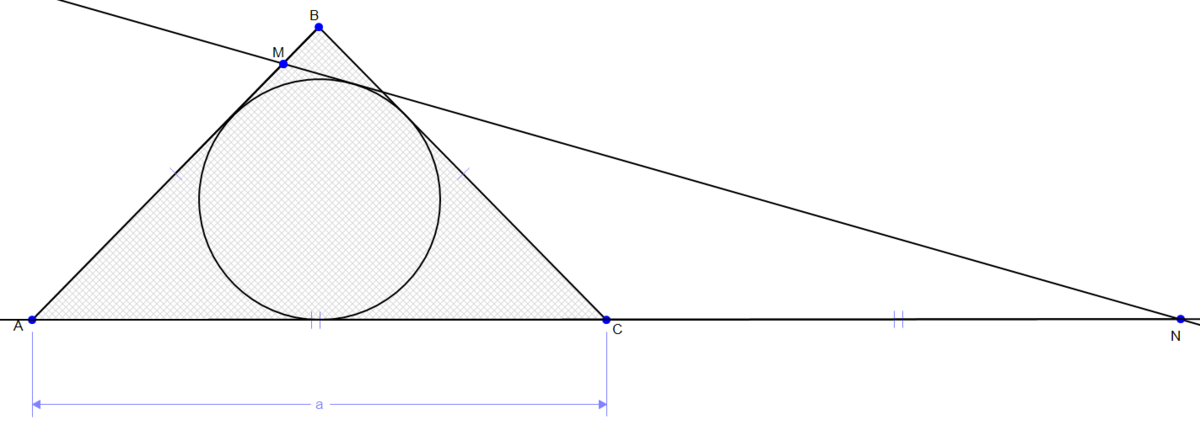
В равнобедренный треугольник ABC (AB=BC) вписана окружность. Через точку M, лежащую на стороне AB, проведена касательная к окружности, пересекающая прямую AC в точке N. Найти боковую сторону треугольника ABC, если AC=CN=a, MB=1/8AB.

Answer 1

Продолжим сторону  $BC$ в два раза , тогда получим параллелограмм $ABNC'$  точка $CC'=b$ ,  заметим теперь что треугольники  $MBO; C'ON$ $O$  точка пересечения $NM$ с $BC$ 
Откуда $BO=frac{OC}{8}\ MO=frac{ON}{8}$ 
Так как касательные проведенные с одной точки равны , то так как $AC$ основание данного треугольника , то  точка касания окружности основанием симметрична , то есть $frac{a}{2}$ 
Если $AF$  $F$  точка касания с  окружностью , стороны  $AB$   $AF=frac{a}{2}$
$AB=b\ AM=b-frac{b}{8}=frac{7b}{8}\ FM=frac{7b}{8}-frac{a}{2}=frac{7b-4a}{8}$
Если $E$   - точка пересечения $MN$ с окружностью   
$ME=FM=frac{7b-4a}{8}$ 
$NE=a+frac{a}{2}=frac{3a}{2}$ ,  по той же причине 
$OE=MO-ME=MO-frac{7b-4a}{8}$ 
с другой стороны
$OE=frac{3a}{2}-ON\ MO-frac{7b-4a}{8}=frac{3a}{2}-ON\ MO=frac{ON}{8}\ \ MN=frac{7b+8a}{8}$
Теперь заметим что окружность вписана   в треугольники 
$AMN;ABC$ 
Положим что угол $BAC=x$
$S_{AMN}=frac{7b*a*sinx *frac{1}{8}}{frac{7b+8a}{16}+frac{7b}{16}+a} \ S_{ABC}=frac{ab*sinx*0.5}{2b+a}$
По формуле $r=frac{S}{p}$ 
подставляя получим 
$ab(7b-5a)=0\ b=frac{5a}{7}$  
это ответ  $frac{5a}{7}$