Предмет: Геометрия,
автор: Аленка050297
Даю 100 баллов.
Основание пирамиды - ромб с периметром 40 см и площадью 60см в квадрате. Все двугранные углы при основании пирамиды равны 60 градусам. Найдите объем пирамиды
Ответы
Автор ответа:
0
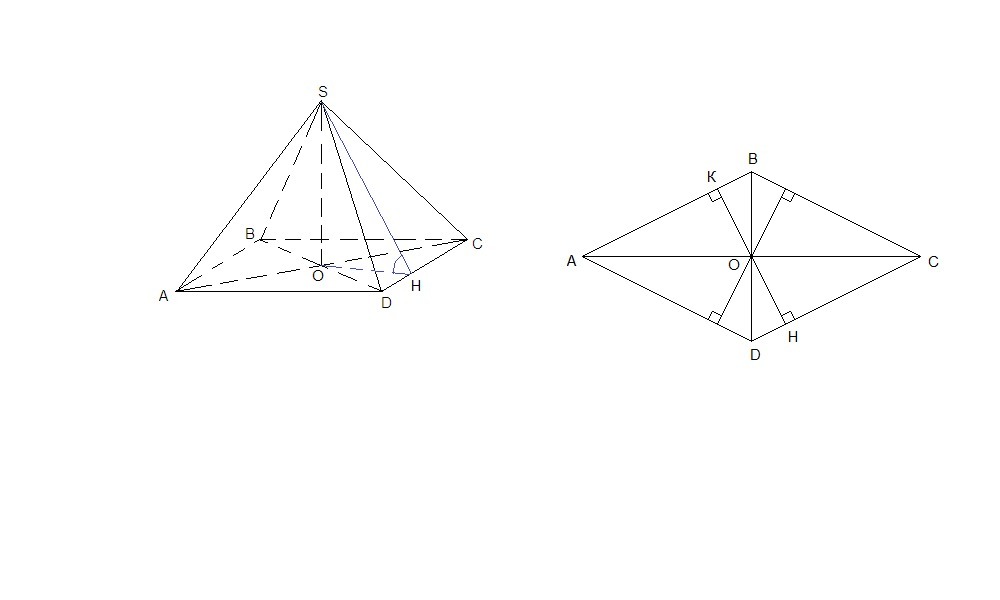
Если двугранные углы при ребрах основания равны (равны углы наклона боковых граней к плоскости основания), то высота пирамиды проецируется в центр окружности, вписанной в основание. В ромбе это точка пересечения диагоналей (точка О на рисунке).
Проведем ОН⊥CD. ОН - проекция наклонной SH на плоскость основания, тогда SH⊥CD по теореме о трех перпендикулярах. Значит
∠SHO = 60° - линейный угол двугранного угла при ребре основания.
Периметр ромба 40 см, значит длина одной стороны ромба
CD = Pabcd/4 = 10 см.
КН - высота ромба.
Sabcd = CD · KH
KH = Sabcd / CD = 60 / 10 = 6 см
ОН = 1/2 КН = 3 см.
ΔSOH: ∠SOH = 90°,
SO = OH · tg∠SOH = 3 · √3 = 3√3 см
Объем пирамиды:
V = 1/3 Sabcd · SO = 1/3 · 60 · 3√3 = 60√3 см³
Приложения:
Похожие вопросы
Предмет: Математика,
автор: anton142435
Предмет: Русский язык,
автор: professor445
Предмет: Қазақ тiлi,
автор: supermarket19092019
Предмет: Алгебра,
автор: Валерия0602
Предмет: Литература,
автор: oksanasavickay