Question

в прямоугольную трапецию вписано круг. найдите площадь трапеции, если её основа равняется a и b.

Answer 1

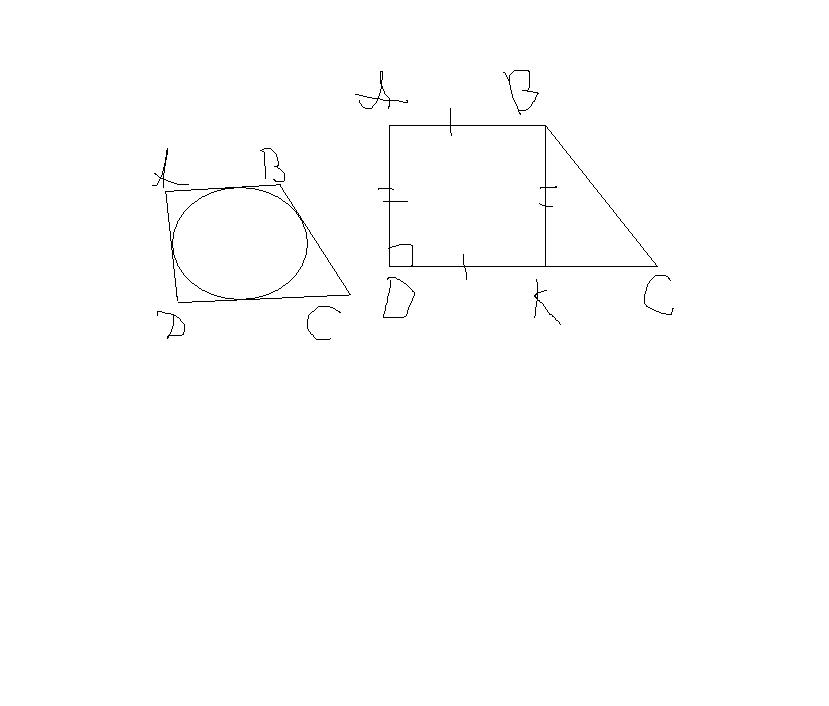
Пусть ABCD - прямоугольная трапеция AB=a, CD=b, a<b

Проведеем высоту BK=AD=h

AB=DK=a, DK=b-a

 

Так как в трапецию вписан круг, то суммы ее противоположных сторон равны, т.е.

AB+CD=AD+BC

откуда (и теоремы Пифагора)

$a+b=h+sqrt{h^2+(b-a)^2};\ (a+b)-h=sqrt{h^2+(b-a)^2};\ a^2+2ab+b^2-2(a+b)h+h^2=h^2+a^2-2ab+b^2;\ 4ab=2(a+b)h;\ h=frac{2ab}{a+b}$

 

Площадь трапеции равна половине произведения суммы оснований на высоту трапеции

$S(ABCD)=frac{(AB+CD)}{2}*AD=frac{a+b}{2}*frac{2ab}{a+b}=ab$

ответ: ав