Предмет: Геометрия,
автор: lizaburdyukova
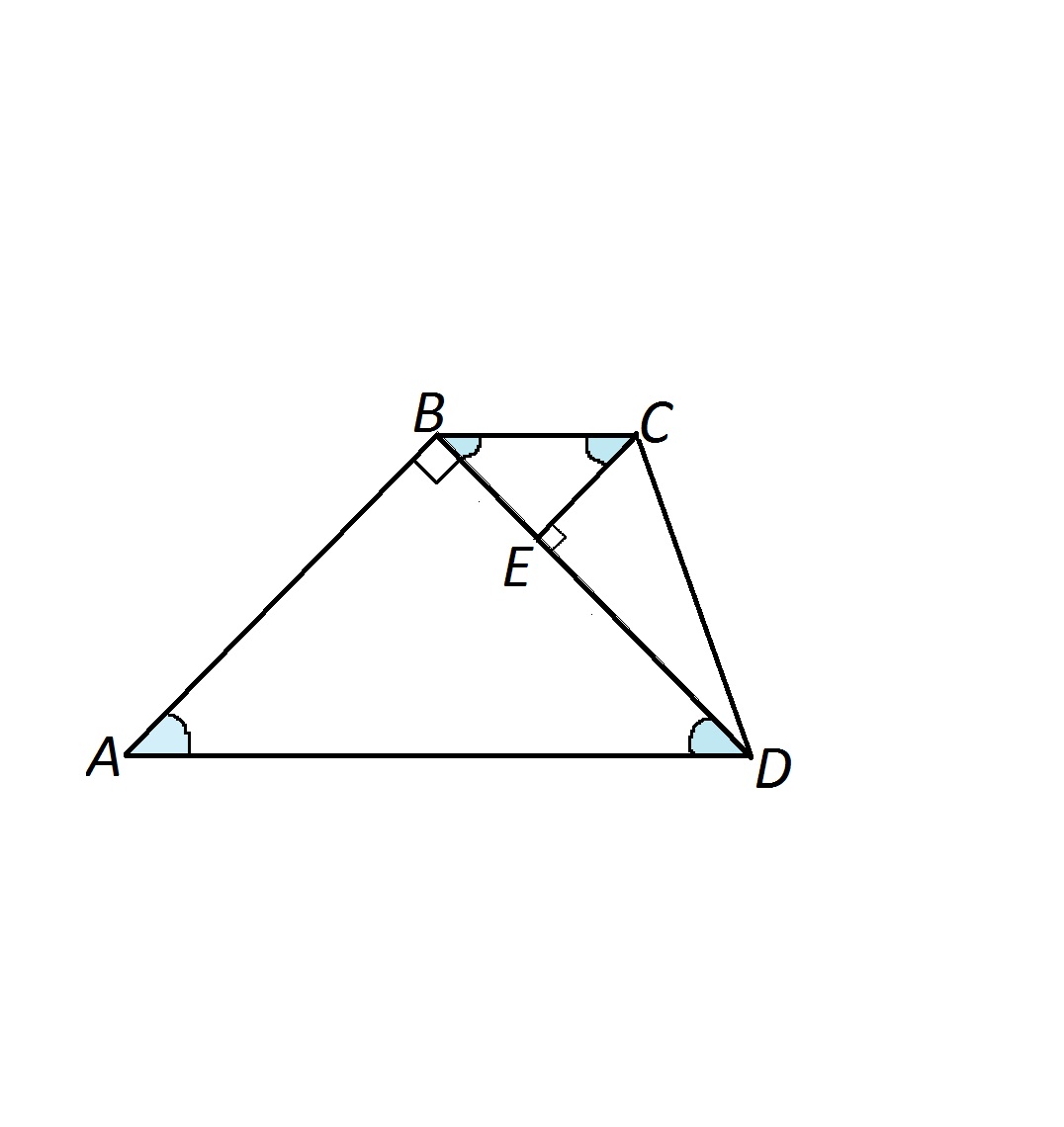
В трапеции ABCD с основаниес BC и AD. AB перпендикулярно BD. BD=2 корня из 5, AD= 2 корня из 10. CE- высота треугольника BCD. Tg угла ECD=3. Найдите BE.
Ответы
Автор ответа:
0
Синус угла ВАD=ВD/АD=(2√5):(2√10)=1/√2=(√2)/2
Это синус 45°.
Угол ВАD=45°, угол АВD - прямой, следовательно, угол ВАD=45° и треугольник АВD равнобедренный.
Угол СВD=углу ВDА как накрестлежащий и равен 45°
( По т.Пифагора АВ также будет равна ВD)
СЕ - высота, СЕ⊥ ВD, след. угол ВСЕ=90°-45° =45°
и треугольник ВЕС равнобедренный, ВЕ=СЕ.
tg угла ECD= 3 ⇒
ЕD:ЕС=3
Но ЕС=ВЕ, следовательно,
ВD:ВЕ=3 ⇒
ВЕ -1 часть, ЕD-3 части.
ВЕ=ВD:4=(2√5):4=(√5):2
Это синус 45°.
Угол ВАD=45°, угол АВD - прямой, следовательно, угол ВАD=45° и треугольник АВD равнобедренный.
Угол СВD=углу ВDА как накрестлежащий и равен 45°
( По т.Пифагора АВ также будет равна ВD)
СЕ - высота, СЕ⊥ ВD, след. угол ВСЕ=90°-45° =45°
и треугольник ВЕС равнобедренный, ВЕ=СЕ.
tg угла ECD= 3 ⇒
ЕD:ЕС=3
Но ЕС=ВЕ, следовательно,
ВD:ВЕ=3 ⇒
ВЕ -1 часть, ЕD-3 части.
ВЕ=ВD:4=(2√5):4=(√5):2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ellajaks888
Предмет: Алгебра,
автор: IVANbombom
Предмет: История,
автор: Аноним
Предмет: Химия,
автор: makis99