Question

При каких значениях параметра а уравнение ax= (модуль x ) + (модуль x -1) имеет ровно 2 решения?

Answer 1

х=0 - не может быть решением данного уравнения, так как

a*0=0

|0|+|0-1|=0+1=1

0 не равно 1

 

перепишем данное уравнение в виде

$a=frac{|x|+|x-1|}{x}$

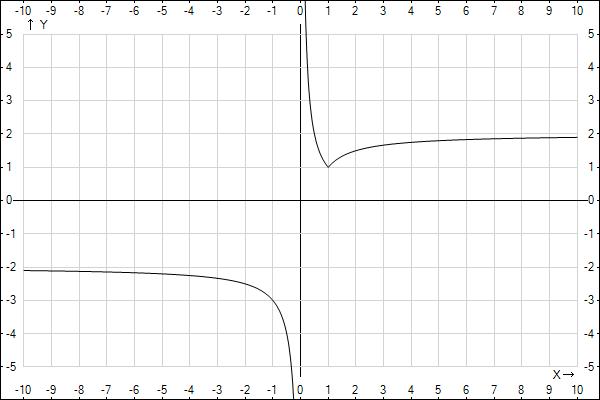
Построим график правой части

$f(x)=frac{|x|+|x-1|}{x}$

при $x geq 1: f(x)=frac{x+(x-1)}{x})=2-frac{1}{x};$

$0 <x$</var></p> <p><img src=[/tex]x <0: :f(x)=frac{-x+(1-x)}{x})=frac{1}{x}-2" title="0 <x" title="x <0: :f(x)=frac{-x+(1-x)}{x})=frac{1}{x}-2" title="0 <x" alt="x <0: :f(x)=frac{-x+(1-x)}{x})=frac{1}{x}-2" title="0 <x" />

$0 <x$

[tex]x <0: :f(x)=frac{-x+(1-x)}{x})=frac{1}{x}-2" />

 

y=a - эта пряммая параллельная оси Ох,

из графика видно, что при a>=2 одно решение (одна точка пересечения)

при 1<a<2 - два решения (две точки пересечения)

при a=1 - одно решение

при -2<=a<1 - нет решений

при a<-2 - одно решение

ответ: при 1<a<2