Предмет: Алгебра,
автор: ximlrf
Логарифмическое уравнение
Приложения:
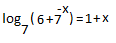
Ответы
Автор ответа:
0
log₇ (6 + 7^(-x)) = 1 + x
ОДЗ: 6 + (1/7)^x > 0, (1/7)^x > - 6
6 + (1/7)^x = 7^(1 + x)
6 + (1/7)^x = 7*( 7^x)
7*7^(2x) - 6* 7^( x) - 1 = 0
7^x = z, z > 0
7z² - 6z - 1 = 0
D = 36 + 4*7*1 = 64
z₁ = (6 - 8)/14
z₁ = - 1/7 не удовлетворяет условию z > 0
z₂ = (6 + 8)/14
z₂ = 1
7^x = 1
7^x = 7^0
x = 0
ОДЗ: 6 + (1/7)^x > 0, (1/7)^x > - 6
6 + (1/7)^x = 7^(1 + x)
6 + (1/7)^x = 7*( 7^x)
7*7^(2x) - 6* 7^( x) - 1 = 0
7^x = z, z > 0
7z² - 6z - 1 = 0
D = 36 + 4*7*1 = 64
z₁ = (6 - 8)/14
z₁ = - 1/7 не удовлетворяет условию z > 0
z₂ = (6 + 8)/14
z₂ = 1
7^x = 1
7^x = 7^0
x = 0
Похожие вопросы
Предмет: Математика,
автор: romastreltsov64
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: fanizakassapchieva
Предмет: Литература,
автор: 1sssn1998