Предмет: Алгебра,
автор: Глухарь
Нужно решить номера 46, 50 , и задание (б)
Приложения:


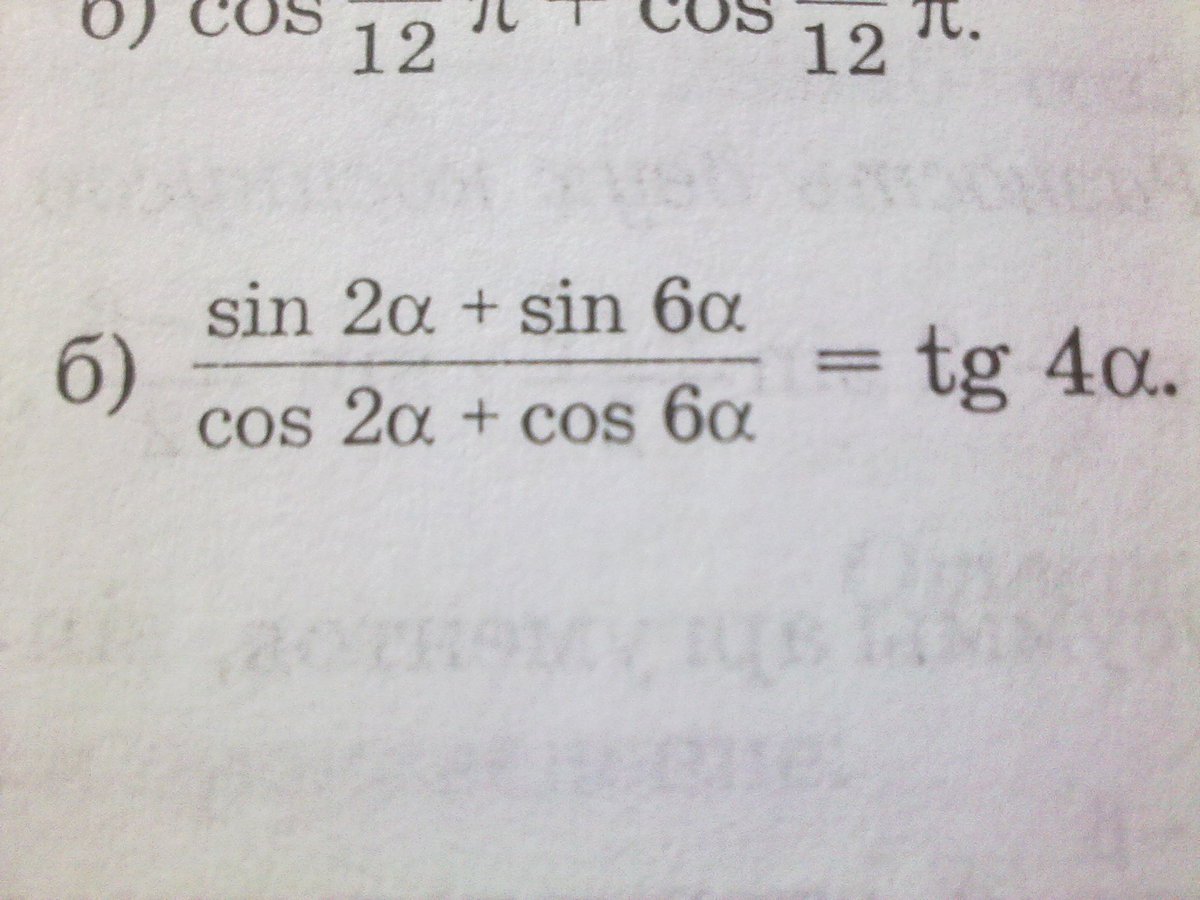
Ответы
Автор ответа:
0
sin(α - 2π/3) - sin(α + 2π/3)=2cos((α-2π/3+α+2π/3)/2)sin((α-2π/3-(α+2π/3))/2) = 2cosαsin(-2π/3)=-2cosαsin(2π/3)=-2cosαsin(π-π/3)=-2cosαsin(π/3)=-√3cosα,
cos(α+π/4)-cos(α-π/4)=-2sin((α+π/4+α-π/4)/2)sin((α+π/4-(α-π/4))/2)=-2sinαsin(π/4)=-√2sinα,
sin(α-π/12)+sin(α-5π/12)=2sin((α-π/12+α-5π/12)/2)cos((α-π/12-(α-5π/12))/2)=2sin(α-π/4)cos(π/6) = √3sin(α-π/4),
cos(α-β)-cos(α+β)=-2sin((α-β+α+β)/2)sin(((α-β-(α+β))/2)=-2sinαsin(-β)=2sinαsinβ;
sin75-sin15=2cos((75+15)/2)sin((75-15)/2)=2cos45sin30=√2/2,
cos11π/12+cos5π/12=2cosπ/3cosπ/4=√2/2,
(sin2α+sin6α)/(cos2α+cos6α)=2sin4αcos(-2α)/(2cos4αcos(-2α))=sin4α/cos4α=tg4α
Похожие вопросы
Предмет: Қазақ тiлi,
автор: judojako3
Предмет: Окружающий мир,
автор: lublubravls
Предмет: Қазақ тiлi,
автор: zenasitun97
Предмет: История,
автор: Олька36