Предмет: Геометрия,
автор: lizavetta95
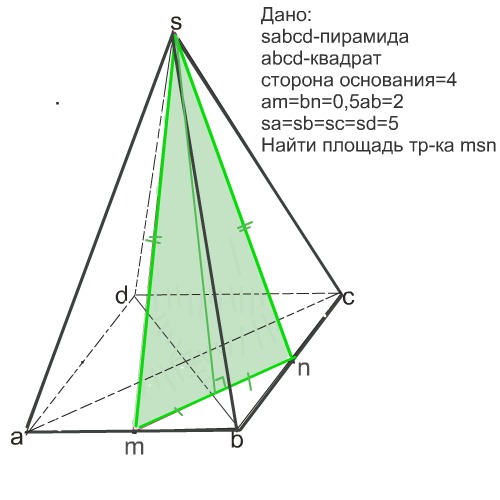
в правильной четырёхугольной пирамиде sabcd с основанием abcd проведено сечение через середины рёбер аb и bc и вершину s . найдите площадь этого сечения если боковое ребро пирамиды=5,а сторона основания равна 4
Ответы
Автор ответа:
0
См. рисунок к задаче.
Площадь сечения равна половине произведения высоты Δ msn на его основание mn
1) mn=1/2 диагонали ас как средняя линия тр-ка abc
ас= √(ab² +bc²)=4√2
mn=2√2
2)
Высота тр-ка msn равна √{ ms²-(mn:2)²
mn:2=√2
ms²= cd²-mb² = 25-4 = 21
Высота тр-ка msn=
√(ms²-(√2)²)=√(21 -2)=√19
S msn=( √19·2√2): 2=√38
----------------------
Вычисления проверила дважды. Результат получился именно таким.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: gundirova67
Предмет: Обществознание,
автор: mishatokarev19
Предмет: Українська мова,
автор: mashaburykina10
Предмет: Математика,
автор: Света27