Предмет: Математика,
автор: Галирон
Докажите, что для произвольных вещественных чисел a,b,c,d,e выполняется неравенство a^2+b^2+c^2+d^2+e^2>=a(b+c+d+e)
Ответы
Автор ответа:
0
Решение задания на фото. Проверяйте на наличие ошибок.
Приложения:
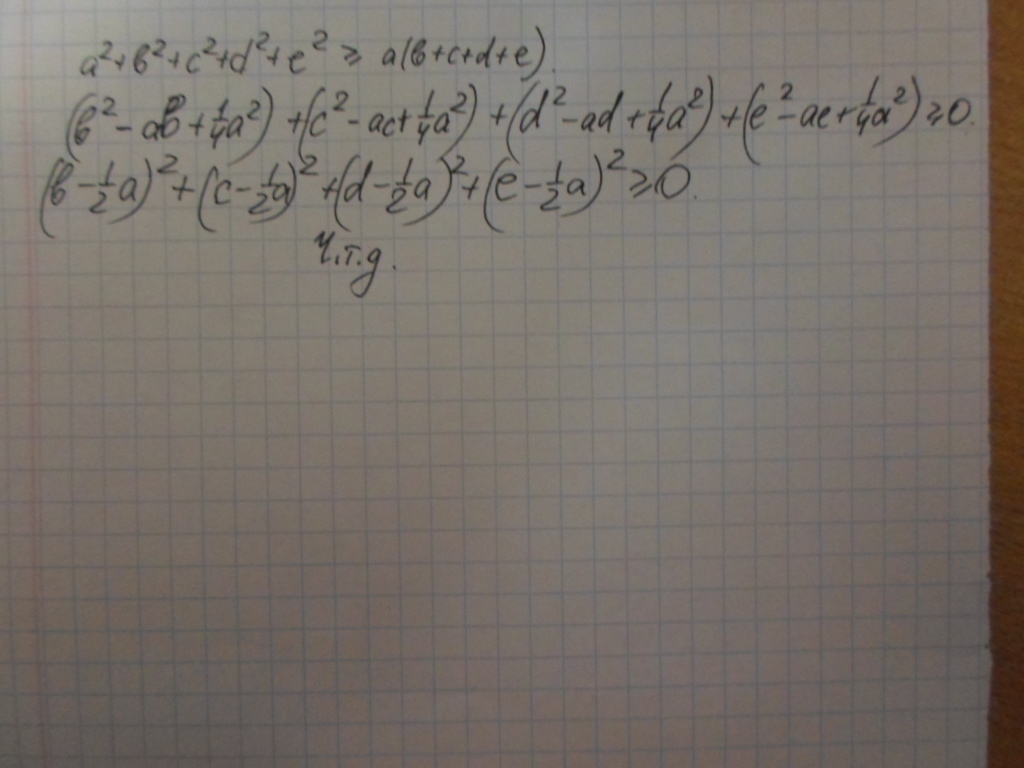
Автор ответа:
0
по тождеству
Приложения:
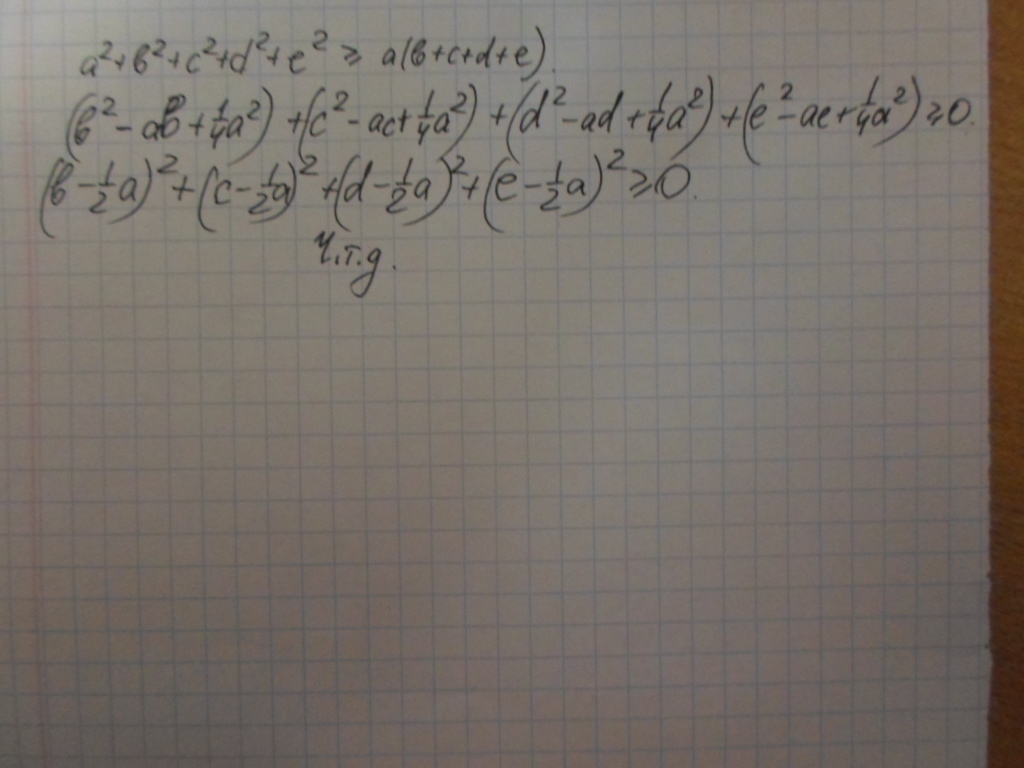
Похожие вопросы
Предмет: Литература,
автор: mbogdan24122012
Предмет: Қазақ тiлi,
автор: aigerimpopova
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: masik2506
Предмет: Математика,
автор: Аноним