Предмет: Математика,
автор: kt1097
Уважаемые знатоки! Нужна ваша помощь, пожалуйста. Награда: желанные 10 баллов!
Заранее благодарю! ;)
"Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45 градусов. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30 градусов и площадь боковой поверхности конуса."
Ответы
Автор ответа:
0
Сечение, проходящее через две образующие - это треугольник. Нам дан угол между ними, следовательно, если мы будем знать длину образующей конуса, мы сможет найти площадь тр-ка по двум сторонам и синус угла между ними.
Найдем длину образующей.
Так как образующая наклонена к плоскости под углом 45, то треугольник, стороны которого высота конуса, радиус конуса и образующая - равнобедренный (чертеж лень вставлять, но, думаю, понятно всё). А значит высота конуса равна его радиусу и равна 10. По теореме Пифагора найдем образующую (это гипотенуза тр-ка)
L²=r²+h²
L²=100+100, значит L=√200=10√2
Площадь тр-ка: S=1/2*a*b*sinC= 1/2*10√2*10√2*sin30=1/2*100*2*1/2=50
Площадь боковой пов-ти конуса: Sбок=π·r·L=10·10√2·π=100√2π
Найдем длину образующей.
Так как образующая наклонена к плоскости под углом 45, то треугольник, стороны которого высота конуса, радиус конуса и образующая - равнобедренный (чертеж лень вставлять, но, думаю, понятно всё). А значит высота конуса равна его радиусу и равна 10. По теореме Пифагора найдем образующую (это гипотенуза тр-ка)
L²=r²+h²
L²=100+100, значит L=√200=10√2
Площадь тр-ка: S=1/2*a*b*sinC= 1/2*10√2*10√2*sin30=1/2*100*2*1/2=50
Площадь боковой пов-ти конуса: Sбок=π·r·L=10·10√2·π=100√2π
Приложения:
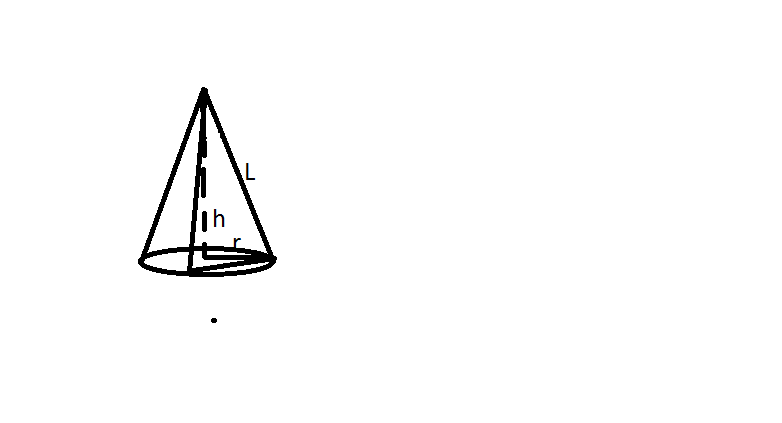
Автор ответа:
0
братан я тебе очень благодарен (что тут добавить?!)) твой ответ обязательно поставлю лучшим! только не мог бы ты пожалуйста чертеж сделать небольшой? извини что так требовательно, просто мне было бы понятнее. я слаб в решении таких задач. спасибо
Автор ответа:
0
попробую
Похожие вопросы
Предмет: Биология,
автор: wowlan6
Предмет: Математика,
автор: znanasha80
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Danila643