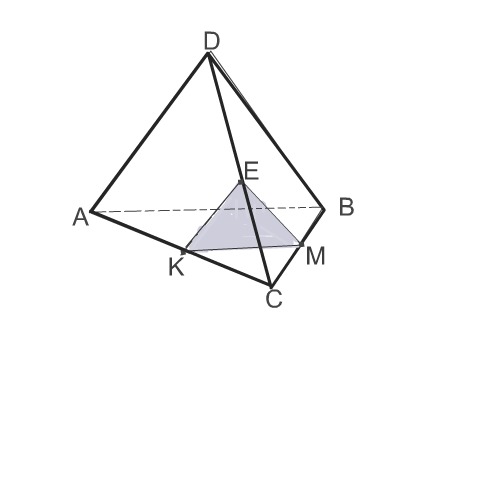
В тетраэдре DABC точки K. E и M являются серединами ребер AC . DC . BC. Докажите , что плоскость KEM параллельна плоскости ADB. Вычислите площадь треугольника ADB . если площадь треугольника KEM равна 27см^2
Ответы
Рассмотрим треугольники ADC, BDC, CDB, составляющие грани тетраэдра. Каждый треугольник проведенным в нем отрезком делится на два подобных треугольника, т.к. тот отрезок - средняя линия треугольника и потому параллелен основанию.
Соединив точки К, Е и М, получим треугольник КЕМ, плоскость которого параллельна плоскости АDВ по свойству пересекающихся прямых:
· Если две пересекающиеся прямые в одной плоскости соответственно параллельны двум пересекающимся прямым в другой плоскости, то и плоскости параллельны.
Δ АDВ и Δ КЕМ подобны по всем трем признакам подобия треугольников.
Отношения площадей подобных треугольников равно квадрату коэффициента их подобия. Так как стороны образующих грани треугольников относятся как 2:1, то площади Δ АDВ и Δ КЕМ относястя как 4:1.
Площадь треугольника ADB больше площади треугольника КЕМ в 4 раза и равна27·4=108 см²