Предмет: Математика,
автор: nesterova1995
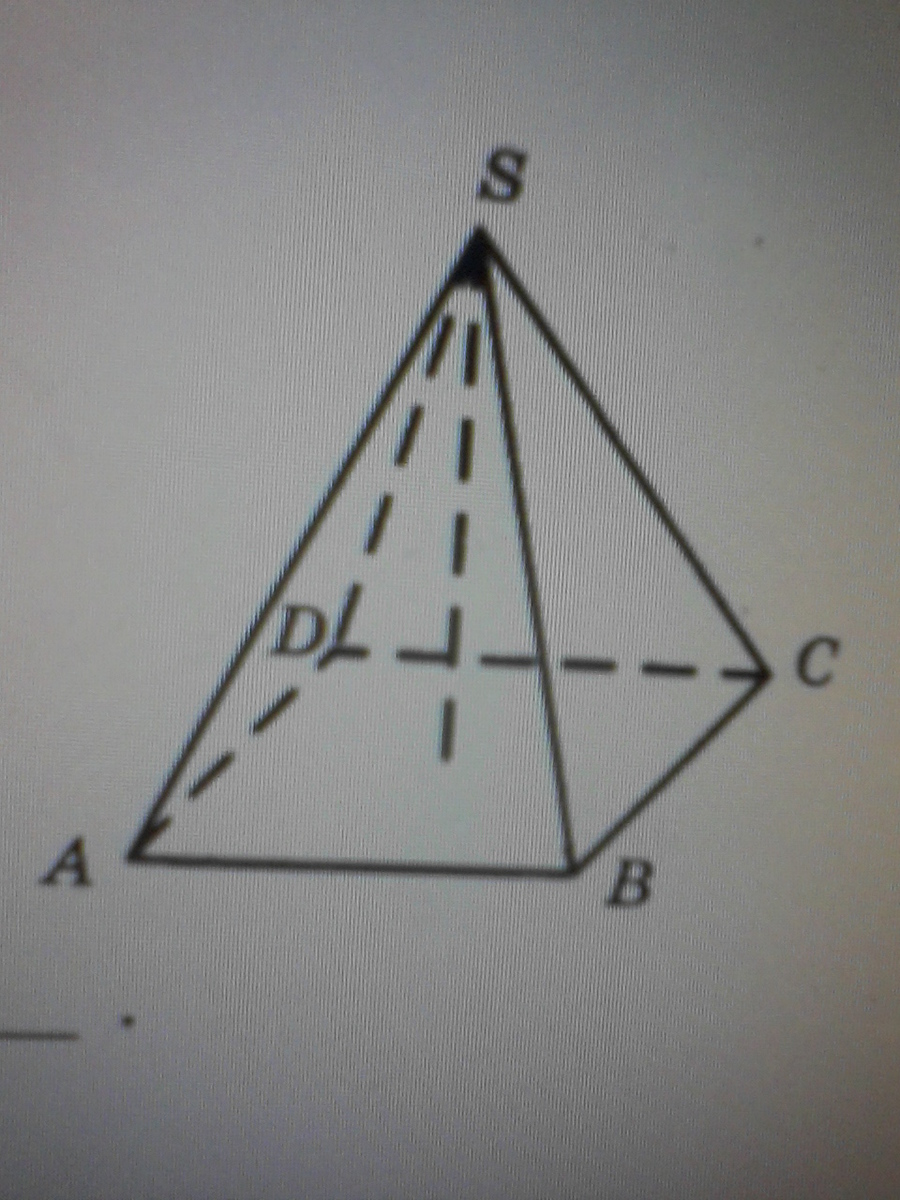
№16 Найдите высоту правильной четырёх-угольной пирамиды, сторона основания которой равна 2, а боковое ребро корень 11.
№ 17 Поставьте в соответствие каждому неравенству множество его решений. Помогите пожалуйста!!!
Приложения:

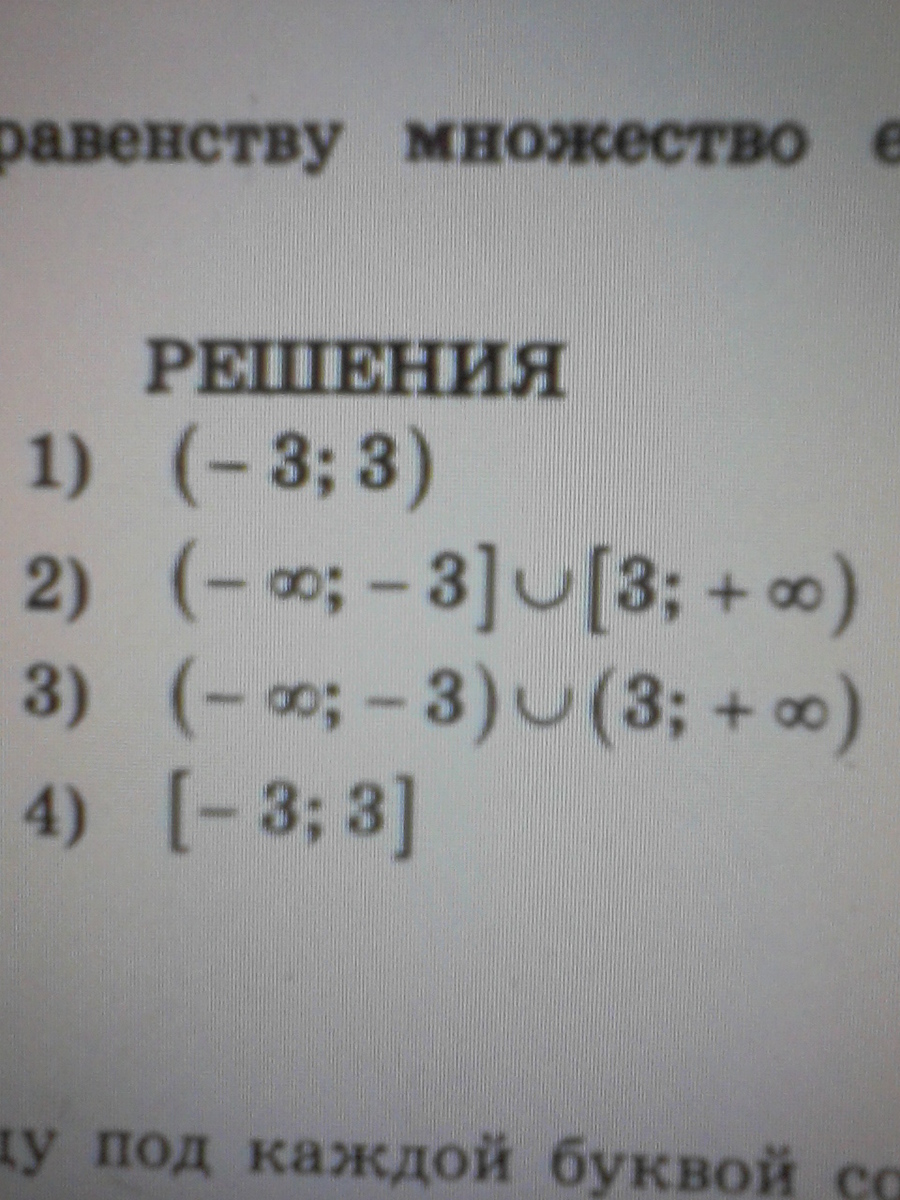
Ответы
Автор ответа:
0
№17
А-2
Б-4
В-3
Г-1
№16
Диагональ основания пирамиды равна а√2, то есть в нашем случае, 2√2.
Высота пирамиды является катетом прямоугольного треугольника, половина диагонали основания - второй катет, а боковое ребро - гипотенуза этого прямоугольного тр-ка. Тогда, по теореме Пифагора,
(√11)²=(√2)²+h². Выразим h
h²=(√11)²-(√2)²=11-2=9 Следовательно высота пирамиды = 3
А-2
Б-4
В-3
Г-1
№16
Диагональ основания пирамиды равна а√2, то есть в нашем случае, 2√2.
Высота пирамиды является катетом прямоугольного треугольника, половина диагонали основания - второй катет, а боковое ребро - гипотенуза этого прямоугольного тр-ка. Тогда, по теореме Пифагора,
(√11)²=(√2)²+h². Выразим h
h²=(√11)²-(√2)²=11-2=9 Следовательно высота пирамиды = 3
Похожие вопросы
Предмет: Химия,
автор: imdebil234
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: polyna201084
Предмет: История,
автор: ludok17
Предмет: Геометрия,
автор: Аноним