Question

Квадраты АВСД и АВС1Д1 лежат в плоскостях, угол между которыми равен 60 градусов.Найдите расстояние между их центрами если АВ=2а

Answer 1

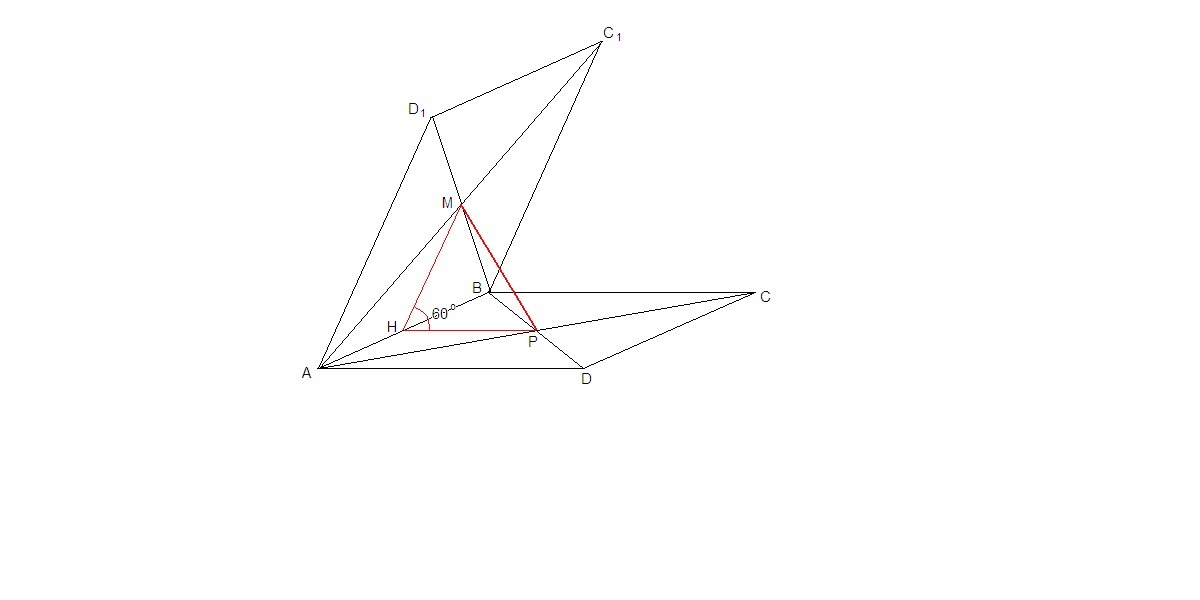
Пусть Н - середина АВ.
Тогда РН - средняя линия треугольника АВС, РН║ВС, а значит РН⊥АВ,
и РН = ВС/2 = а.
МН - средняя линия треугольника АВС₁, МН║ВС₁, ⇒ МН⊥АВ, и
МН = ВС₁/2 = а.

∠МНР = 60° - линейный угол двугранного угла между плоскостями квадратов.
ΔМНР: РН = МН = а и ∠МНР = 60°, значит треугольник равносторонний, ⇒
МР = а.