Предмет: Алгебра,
автор: Эльдар000
помогите решить срочно нужно решите один из них плизз дам все свои баллы
Приложения:
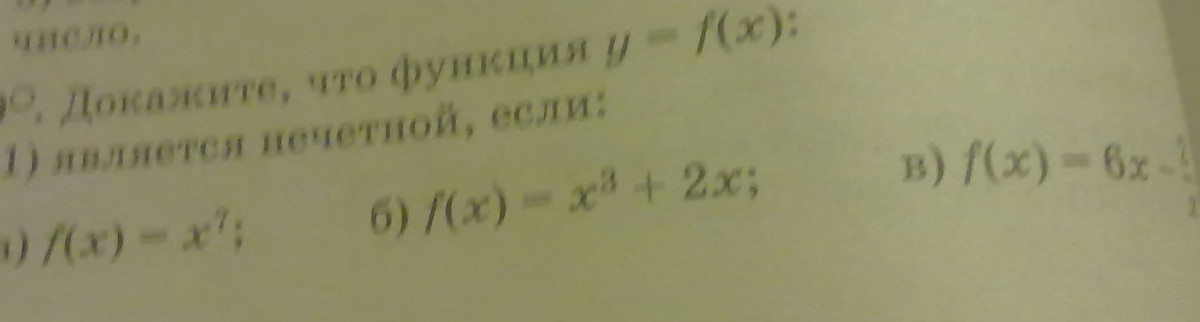

Ответы
Автор ответа:
0
Для проверки четности и нечетности функции вместо х в формулу подставляют (-х), если формула не меняется, то функция - четная, есди знак (-) можно вынести за скобку, то - нечетная, а если ничего сделать нельзя, то функция ни четная, ни нечетная. Решаем
f([)=x^7 меняем х на -х f(-x)=(-x)^7=-x^7 функция нечетная
f(x)= x^2 =2x меняем х на -х f(-x)=(-x)^2-2x=x^2-2x функция ни четная ни нечетная
f([)=x^7 меняем х на -х f(-x)=(-x)^7=-x^7 функция нечетная
f(x)= x^2 =2x меняем х на -х f(-x)=(-x)^2-2x=x^2-2x функция ни четная ни нечетная
Автор ответа:
0
а) f(x)=x⁷
f(-x)=(-x)⁷=-x⁷
Так как f(-x)=-f(x), то f(x) - нечетная
б) f(x)=x³+2x
f(-x)=(-x)³+2(-x)=-x³-2x=-(x³+2x)
Так как f(-x)=-f(x), то f(x) - нечетная
в) f(x)=6x - 2
x
f(-x)=6*(-x) - 2 = -6x+ 2 = - (6x - 2)
-x x x
Так как f(-x)=-f(x), то f(x) - нечетная
2)
а) f(x)=x⁸
f(-x)=(-x)⁸=x⁸
Так как f(-x)=f(x), то f(x) - четная
б) f(x)=x⁴-5x²+1
f(-x)=(-x)⁴-5(-x)²+1=x⁴-5x²+1
Так как f(-x)=f(x), то f(x) - четная
в) f(x)=3- 7
x²
f(-x)=3 - 7 = 3 - 7
(-x)² x²
Так как f(-x)=f(x), то f(x) - четная
3.
a) f(x)=x⁸-x⁷
f(-x)=(-x)⁸ - (-x)⁷=x⁸+x⁷
Так как f(-x)≠f(x) и f(-x)≠-f(x), то функция никакая.
б) f(x)=3x²-5x-4
f(-x)=3(-x)²-5(-x)-4=3x²+5x-4
Так как f(-x)≠f(x) и f(-x)≠-f(x), то функция никакая.
f(-x)=(-x)⁷=-x⁷
Так как f(-x)=-f(x), то f(x) - нечетная
б) f(x)=x³+2x
f(-x)=(-x)³+2(-x)=-x³-2x=-(x³+2x)
Так как f(-x)=-f(x), то f(x) - нечетная
в) f(x)=6x - 2
x
f(-x)=6*(-x) - 2 = -6x+ 2 = - (6x - 2)
-x x x
Так как f(-x)=-f(x), то f(x) - нечетная
2)
а) f(x)=x⁸
f(-x)=(-x)⁸=x⁸
Так как f(-x)=f(x), то f(x) - четная
б) f(x)=x⁴-5x²+1
f(-x)=(-x)⁴-5(-x)²+1=x⁴-5x²+1
Так как f(-x)=f(x), то f(x) - четная
в) f(x)=3- 7
x²
f(-x)=3 - 7 = 3 - 7
(-x)² x²
Так как f(-x)=f(x), то f(x) - четная
3.
a) f(x)=x⁸-x⁷
f(-x)=(-x)⁸ - (-x)⁷=x⁸+x⁷
Так как f(-x)≠f(x) и f(-x)≠-f(x), то функция никакая.
б) f(x)=3x²-5x-4
f(-x)=3(-x)²-5(-x)-4=3x²+5x-4
Так как f(-x)≠f(x) и f(-x)≠-f(x), то функция никакая.
Похожие вопросы
Предмет: Другие предметы,
автор: morgunenkosasha1911
Предмет: Математика,
автор: limonman4ik
Предмет: Українська мова,
автор: egorhazamov
Предмет: Геометрия,
автор: lerka2112