Предмет: Геометрия,
автор: tyaroslava1
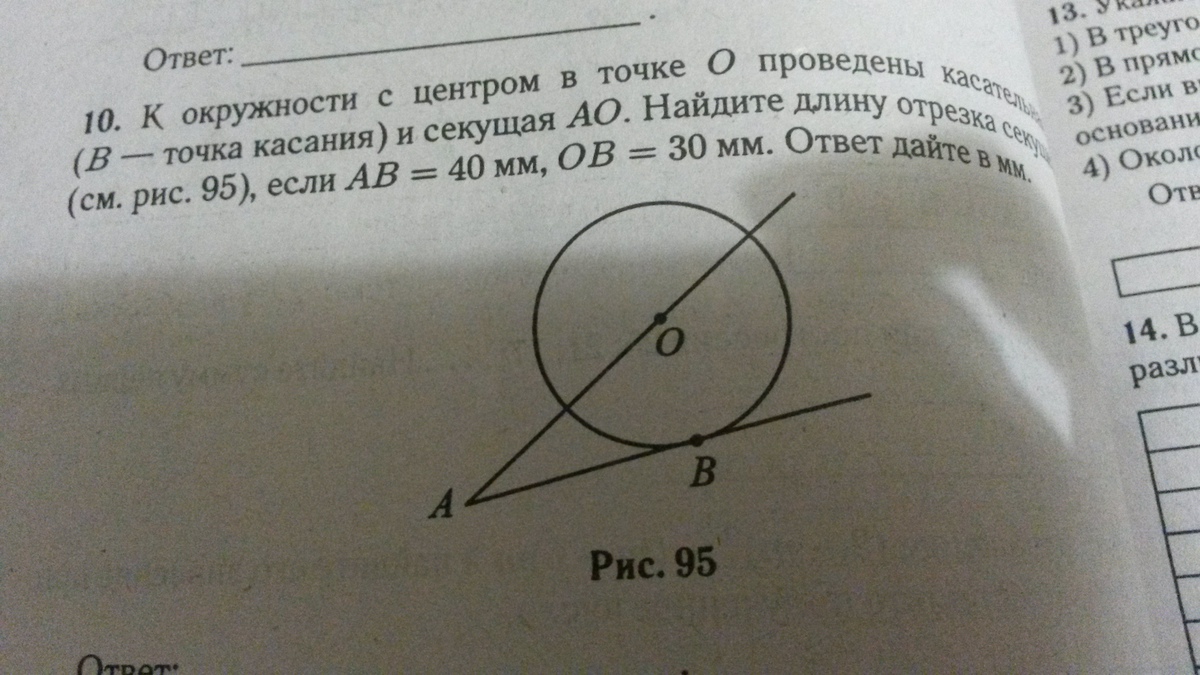
К окружности с центром в точке О
проведены касательная АВ(В-точка касания) и секущая АО. Найдите длину отрезка секущей АО, если AB= 40мм, OB=30мм. Ответ должен быть 50
Приложения:
Ответы
Автор ответа:
0
Квадрат отрезка касательной равен произведения секущей на ее внешнюю часть
АВ²=х*(х+60) т.к. Радиус равен 30, диаметр 60, верхняя часть секушей равна х, а вся секущая х+60
х²+60х-1600=0
Д=900+1600=2500
х1=-30+50=20 х2=-30-50=-80
Отрезок секущей ОА=20+30=50
АВ²=х*(х+60) т.к. Радиус равен 30, диаметр 60, верхняя часть секушей равна х, а вся секущая х+60
х²+60х-1600=0
Д=900+1600=2500
х1=-30+50=20 х2=-30-50=-80
Отрезок секущей ОА=20+30=50
Автор ответа:
0
Спасибо)
Похожие вопросы
Предмет: Математика,
автор: nurersultan4
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: apastuhova91
Предмет: География,
автор: Nastya8brick